vector dot product
向量的计算...
向量的内积与外积
点与点的减法
- 描述的是起点到终点的运动
点\({p}\)与向量\(\vec{a}\)的加法
- 从\(P\)出发经过这个向量\(\vec{a}\)代表的运动,到达一个新的点\(P_0\)
在此处定义两个向量
- \(\vec{a}\) \[ \vec{a} = \begin{bmatrix} a_1 \\ a_2 \\ a_3 \\ \end{bmatrix} \]
- \(\vec{b}\) \[ \vec{b} = \begin{bmatrix} b_1 \\ b_2 \\ b_3 \\ \end{bmatrix} \]
向量点击
- 点击(内积)的公式 \[\vec{a}\cdot\vec{b} = |\vec{a}|\times|\vec{b}|\times \cos \theta \] \[ \vec{a}\cdot\vec{b} = \sum_{i=1}^{n} \left\{ a_i * b_i \right\}\]
- 点击的几何意义
其中一个向量在另一个向量上的投影且与点击的顺序无关
- \(\vec{a}\cdot\vec{b} > 0\) 方向基本相同,夹角在0°到90°之间
- \(\vec{a}\cdot\vec{b} = 0\) 正交,相互垂直
- \(\vec{a}\cdot\vec{b} < 0\) 方向基本相反,夹角在90°到180°之间
- 点击的巧用
- 计算向量的模长的平方 \[|\vec{a}|^2 = \vec{a} \cdot \vec{a} \]
- 计算两个向量之间的夹角的\(\cos\theta\) -
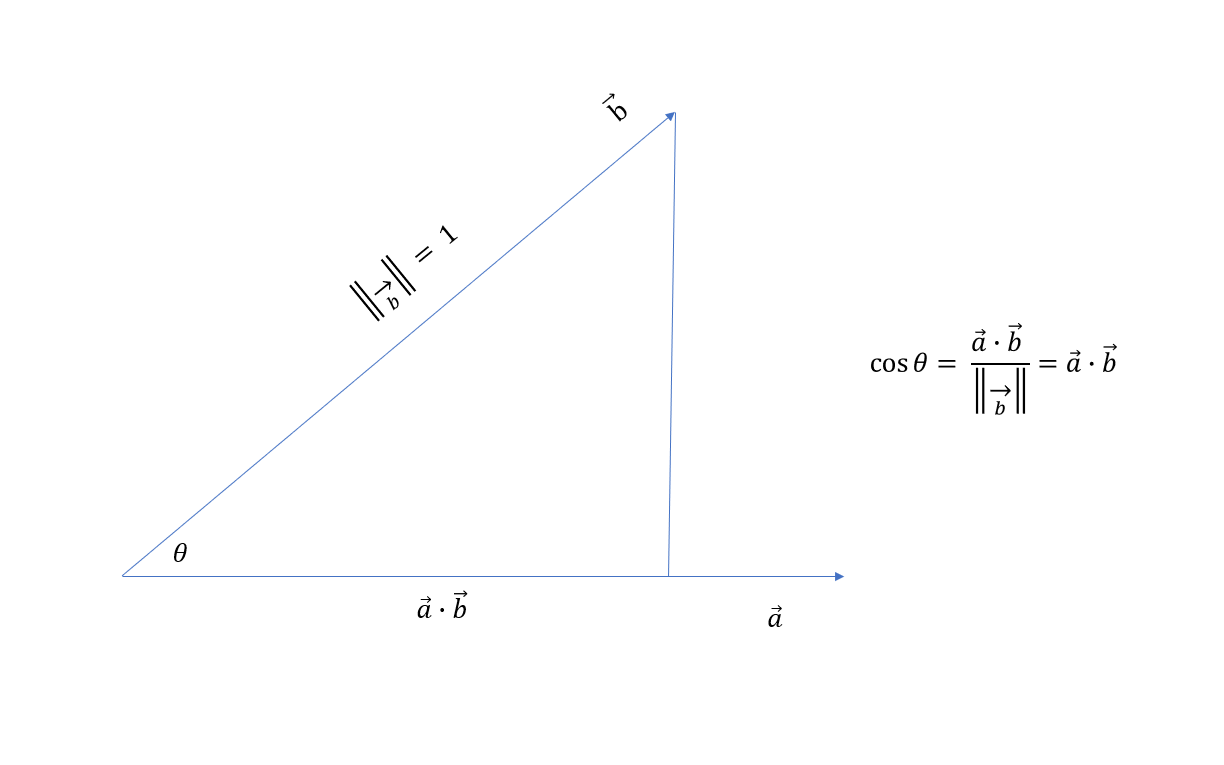
- 两个单位向量的点击等于他们的夹角的\(\cos\theta\)的值
- 两个互相垂直的向量的点击总是为
0\(\theta = 90^0\) \[\vec{a} \cdot \vec{b} = |\vec{a}| \ast |\vec{b}| \ast \cos\theta = 0 \] - 一条射线描述的向量[起点 +
方向]点击一个平面的法向可以得到起点到平面的距离
### 向量叉积
- 外积公式 \[ \vec{a} \times \vec{b} = \begin{bmatrix} a_2 * b_3 - b_2 * a_3 \\ a_3 * b_1 - b_3 * a_1 \\ a_1 * b_2 - b_1 * a_2 \\ \end{bmatrix} \]
- 叉积的几何意义
- 几何表达公式 \[
\vec{a} \times \vec{b} = |\vec{a}| * |\vec{b}| * sin(\theta) * \vec{n}
\]
- \(\vec{n}\) 表示\(\vec{a}\), \(\vec{b}\)所构成平面的法向量方向的单位向量
- 在二维空间中:叉积得到的向量的模长\(|\vec{a}\times\vec{b}|\)等于这两个向量\(\vec{a},\vec{b}\)组成的平行四边形的面积
- 几何表达公式 \[
\vec{a} \times \vec{b} = |\vec{a}| * |\vec{b}| * sin(\theta) * \vec{n}
\]
- 外积的使用
- 外积的模长则为夹角的正弦(始终为正)
扩展知识
- 扩展 - 1
- 平面上的四个点\(P_1\),\(P_2\),\(P_3\),\(P_4\),分别构成向量 \(\vec{P_1P_2}\)与\(\vec{P_3P_4}\)。如何通过点击计算他们交点的坐标?
- 下次吧!