View/Camera Transformation
计算机图形学的视图变换过程的解析...
视图变换
- 视图变换是将所有世界空间中的点,变换到视图空间下的操作
- 这种变换,我们通过矩阵可以轻易的完成,但是我们首先需要计算一个描述这种变换的矩阵
- 在一般的实现中,我们将视图变换的过程抽象出了一个相机的概念
- 本身而言在图形学中是没有相机这个概念的
视图变换-变换过程
- 从顶点构建到最终渲染成一张二维的图片,在行业中大家将之类比为拍照的行为
- 模型变换 - 取景的过程
- 视图变换 - 摆放相机的过程
- ......
- 此处我们只是讨论视图变换的过程
定义一个相机
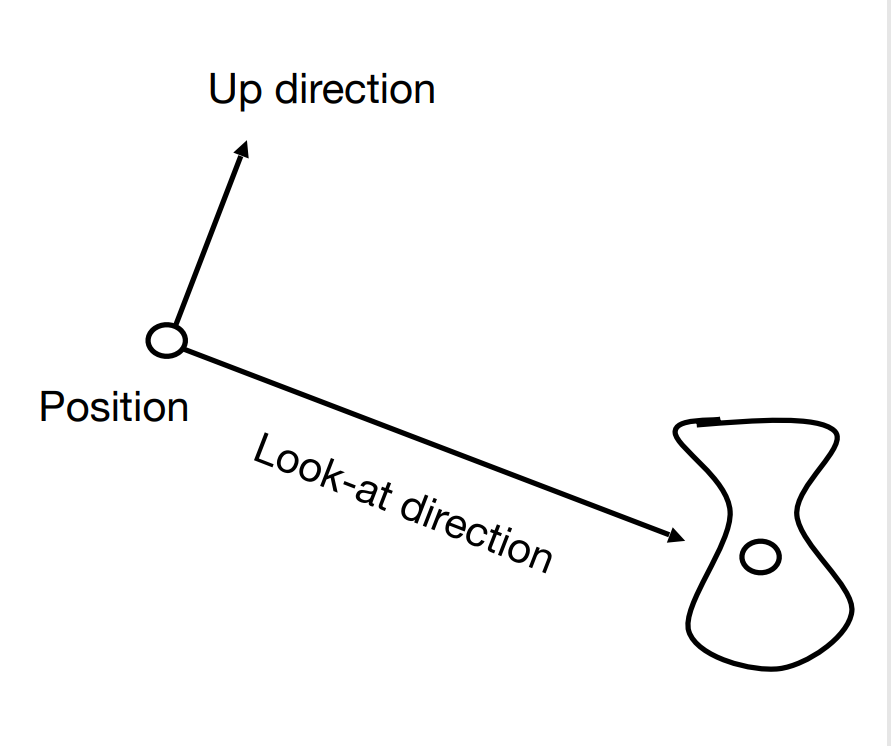
- 对于上述的那个拍照的行为,我们要拍摄这个摆放好的景物,关于相机我们只需要关心三个方面。
- 我们基于右手系考虑下面的这些信息
- 相机的位置 \(e\) -> \(eye\) = $x,y,z,1$
- 相机的看的方向,既相机的拍摄方向 \(\vec{dir}\) -
lookAt direction$x,y,z,0 $ - 相机的上方向 \(\vec{up}\) = \(\lbrace x,y,z,1\rbrace\)
- 大概是手机横屏与竖屏的区别
- 我们获得一个观察方向,一个向上的方向
- 观察方向与向上方向垂直
- 通过叉积我们可以得到一个向右的方向\(\vec{right}\)
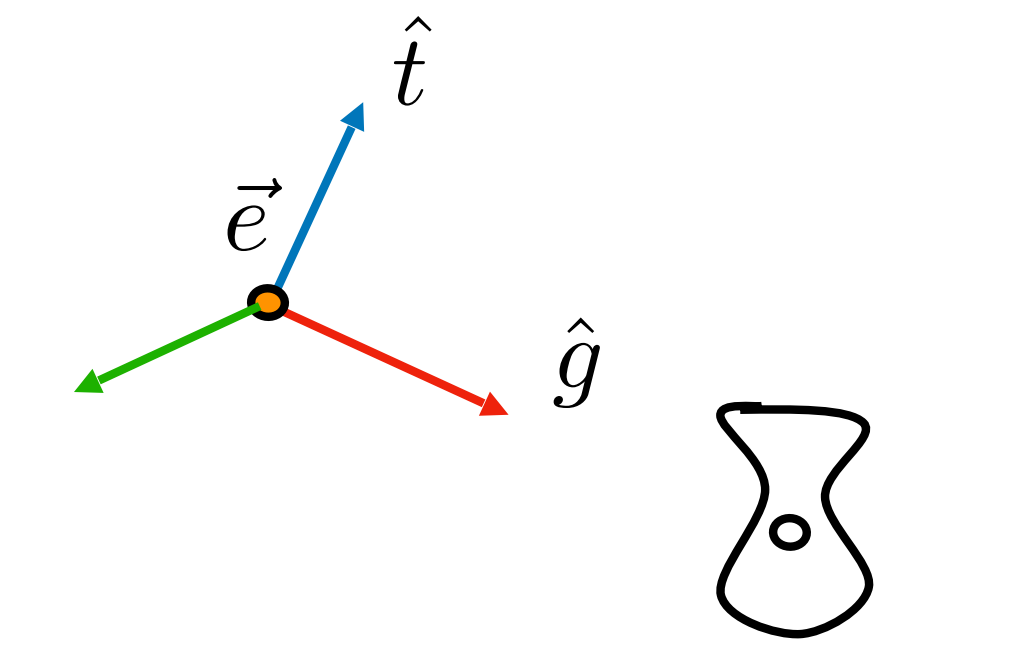
从拍照的行为来看,相机的观察方向是指向模型摆放的位置,我们保持两个物体的相对位置关系(相机与场景),相机做了某种变换,模型也跟着做同样的变换。基于这种相对位置的变化,我们约定,将相机永远变换到原点,相机的观察方向永远是
-z 方向,以此我们构建一个坐标系
计算视图变换矩阵
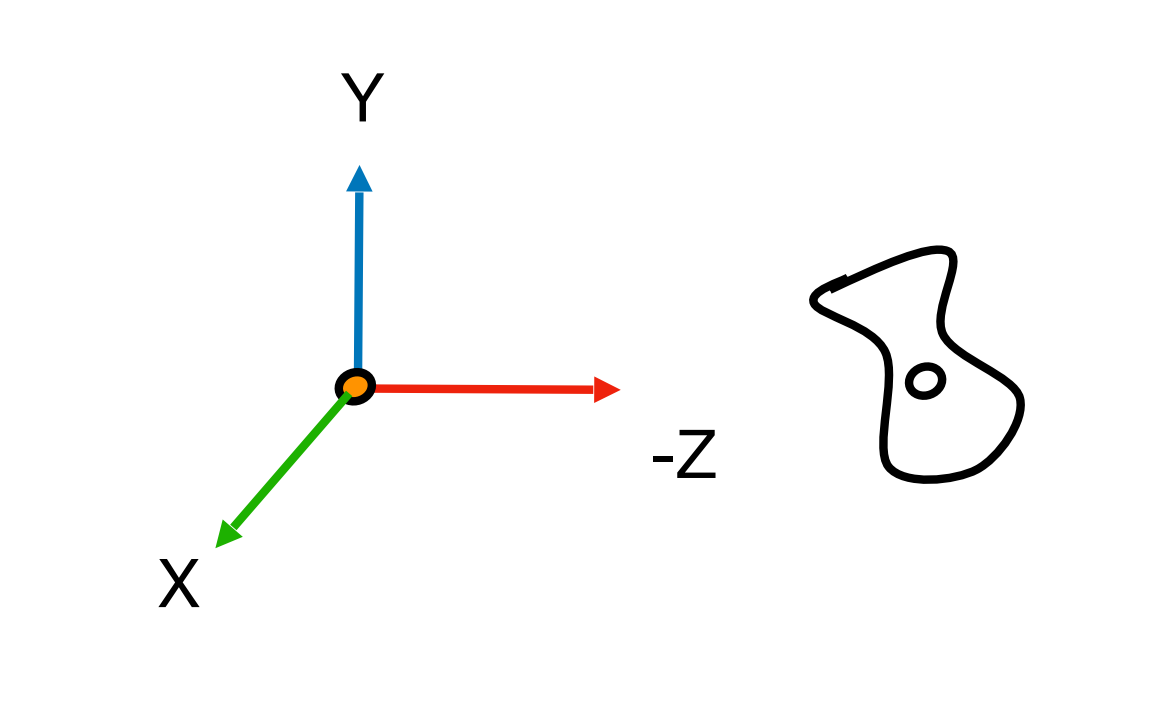
- 我们将以相机定义的坐标框架通过旋转与平移将之与世界空间的坐标重合
- \(\vec{g}\) -> $ $
- \(\vec{t}\) -> $ $
- \(\vec{t} \times \vec{g}\) -> \({\vec{X}}\)
- 但是我们要做到上面的事情比较困难,换一种思路,我们做相反的事情
- 我们将世界空间的坐标通过旋转&平移将之与相机定义的坐标系重合
- \(\vec{Y}\) -> \(\vec{t}\)
- \(\vec{-Z}\) -> \(\vec{g}\)
- \({\vec{X}}\) -> \(\vec{t} \times \vec{g}\)
- 构建一个旋转矩阵的逆矩阵,然后计算逆矩阵的逆便得到我们想要的矩阵。
- 由于坐标系的三个轴是正交的,我们只需要将矩阵转置就可以得到这个旋转矩阵。
- 将旋转矩阵与平移矩阵乘起来,就得到想要的试图变换矩阵

上述过程描述了视图变换的过程与视图矩阵的计算。