透视矩阵计算

发表于 2022-09-08 更新于 2023-01-09 分类于 Computer Graphics

在经过投影变换后，场景由三维变换到二维，这过程如何实现呢？关于两种不同的投影方式计算生成对应的投影矩阵，该如何计算？

投影变换

平行投影
透视投影

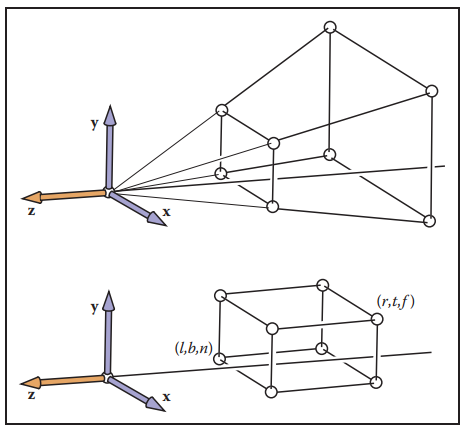
当我们完成视图变换
- 相机被移动到世界坐标系的原点，同时场景做了同样的相对位移。
- 相机看向-z方向，我们指定了一个up,通过cross我们分别计算出三个轴向，相当远将世界坐标系做一个旋转操作，变换到$\vec{right},\vec{up},\vec{look}$ - 相机右方向，上方向，观察方向，场景也要做相同的旋转操作
- 下一步的操作便是投影
此时，我们的场景变换到了相机描述的坐标系下。

1. 平行投影

我们最先要做的是定义一个视锥体。
- $[left,right]$
- $[bottom,top]$
- $[zNear,ZFar]$
- $ortho(left,right,bottom,top,zNear,zFar)$
- 由于相机朝向-z,实际上说zNear 大于zFar.
如上图平行投影与透视投影所示：平行投影没有近大远小的视觉效果，我们可以简单的丢掉所有顶点的Z值，将他们挤压到一个平面上，就可以得到一个平面的图。这将会丢掉维度信息，且不可逆，将场景变为二维，同是，对于关于XOY平面对称的点相当不友好[-z,z]，所以并不是一个合适的方法。
- 变换矩阵: \[ P_0 = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \]
更好的做法是将场景移动到原点，然后做一次缩放，将场景的所有的顶点的坐标变换到$(x,y,z) \in [-1,1]^3$
- 此时将会生成 z-buffer，三维场景的信息变为$[x,y]^2$的信息

对应矩阵
- T matrix \[ T = \begin{bmatrix} 1 & 0 & 0 & -\frac{left+right}{2}\quad \\ 0 & 1 & 0& -\frac{top+bottom}{2}\quad \\ 0 & 0 & 1 & -\frac{zNear+zFar}{2}\quad \\ 0 & 0 & 0 & 1 \end{bmatrix} \]
- S matrix \[ S = \begin{bmatrix} \frac{2}{right - left}\quad & 0 & 0 & 0 \\ 0 & \frac{2}{top - bottom}\quad & 0 & 0 \\ 0 & 0 & \frac{2}{zFar - zNear}\quad & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \]
- Ortho Matrix \[ Ortho = S \times T = \begin{bmatrix} \frac{2}{right - left}\quad & 0 & 0 & 0 \\ 0 & \frac{2}{top - bottom}\quad & 0 & 0 \\ 0 & 0 & \frac{2}{zFar - zNear}\quad & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \times \begin{bmatrix} 1 & 0 & 0 & -\frac{left+right}{2}\quad \\ 0 & 1 & 0& -\frac{top+bottom}{2}\quad \\ 0 & 0 & 1 & -\frac{zNear+zFar}{2}\quad \\ 0 & 0 & 0 & 1 \end{bmatrix} \\ = \begin{bmatrix} \frac{2}{right - left}\quad & 0 & 0 & -\frac{left+right}{2}\quad \\ 0 & \frac{2}{top - bottom}\quad & 0 & -\frac{top+bottom}{2}\quad \\ 0 & 0 & \frac{2}{zFar - zNear}\quad & -\frac{zNear+zFar}{2}\quad \\ 0 & 0 & 0 & 1 \end{bmatrix} \]

2. 透视投影

透视投影变换的过程可以认为是将透视投影定义的视椎体挤压成一个长方体,然后运用平行投影相似的变换(S + T)

2.1. 挤压矩阵计算

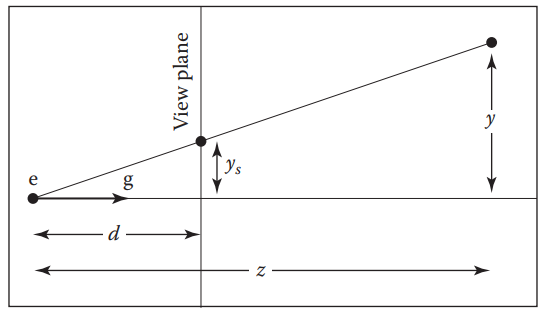- 如图projection2ortho,从侧面上看: - $\vec{g}$ 指向-Z方向 - $d$ & $y_s$构成的三角形在$e$的角度为fov的一半 - 压缩是将$y$压缩到$y_s$

2.1.1 $[X_{far},Y_{far}]$ to $[X_{near},Y_{near}]$

\[ \begin{pmatrix} x \\ y \\ z \\ \end{pmatrix} * \begin{bmatrix} 1 & 0 & 0 \\ 0 & n & 0 \\ 0 & 0 & 1 \\ \end{bmatrix} = \begin{pmatrix} x \\ y_s \\ z \\ \end{pmatrix} \]

由三角形相似可以得到: $\frac{y_s}{y}\quad=\frac{n}{f}\quad$ => $y_s = \frac{n}{f}\quad * y$
同理: $\frac{x_s}{x}\quad$=$ $ => $x_s = \frac{n}{f}\quad * x$

2.1.2. 挤压过程

将一个点由透视投影的视椎体变换到正交下: \[ \begin{pmatrix} x \\ y \\ z \\ 1 \end{pmatrix} => \begin{pmatrix} \frac{n}{f}\quad*{x} \\ \frac{n}{f}\quad * y \\ {???} \\ 1 \end{pmatrix} => \begin{pmatrix} n * x \\ n * y \\ {???} \\ f \end{pmatrix} \]

\[Mat4^{(4\times4)}_{p->o} = \begin{bmatrix} n & 0 & 0 & 0 \\ 0 & n & 0 & 0 \\ c_1 & c_2 & c_3 & c_4 \\ 0 & 0 & 1 & 0 \end{bmatrix}\]

考虑当被变换的这个点在近平面中心上: \[\begin{pmatrix} n * x \\ n * y \\ {???} \\ f \end{pmatrix} => \begin{pmatrix} \\ x \\ y \\ n \\ 1 \end{pmatrix} = \begin{pmatrix} n*x \\ n*y \\ n^2 \\ n \end{pmatrix} \]

\[ Mat4^{(4\times4)}_{p->o} * \begin{pmatrix} x \\ y \\ n \\ 1 \end{pmatrix} = \begin{pmatrix} n*x \\ n*y \\ n^2 \\ n \end{pmatrix} \]

得到: $c_1 * x + c_2 * y + c_3 * n + c_4 * 1 = n^2$
得到: $c_3 * n + c_4 = n^2$

同理考虑这个点落在远平面的中心:
得到: $c_3 * f + c_4 = f^2$
解得:
- $c_3$ \[ c_3 = n + f \\ \]
- $c_4$ \[ c_4 = -n * f \]
$Mat4^{(4\times4)}_{p->o}$

\[Mat4^{(4\times4)}_{p->o} = \begin{bmatrix} n & 0 & 0 & 0 \\ 0 & n & 0 & 0 \\ 0 & 0 & n + f & -n*f \\ 0 & 0 & 1 & 0 \end{bmatrix} \]

2.1.3. 完整的透视变换矩阵

$Mat^{(4\times4)}_{p->o} * Ortho^{4\times4}_{ortho}$ \[ Mat^{4\times4}_{per} = \begin{bmatrix} \frac{2*n}{right - left}\quad & 0 & \frac{right + left}{right - left}\quad & -\frac{left+right}{2}\quad \\ 0 & \frac{2*n}{top - bottom}\quad & \frac{top + bottom}{bottom - top}\quad & 0 \\ 0 & 0 & \frac{zFar + zNear}{zNear - zFar}\quad & -\frac{2*zFar*zNear}{zFar - zNear}\quad \\ 0 & 0 & 1 & 0 \end{bmatrix} \]