光先追踪的加速方法就是引入层次结构数据结构，计算光线与层次结构的相交，从而加速光线与场景的求交。
OBB与Ray求交
- 我们在更之前的地方定义了一个
OBB,往前翻一番也许就能找到
- \(center\) - 盒子的中心点
- \(\vec{u}\) - 盒子的某个法线 \(u\)
- \(\vec{v}\) - 盒子的某个法线 \(v\)
- \(\vec{w}\) - 盒子的某个法线 \(w\)
- 盒子的尺寸 - \(size\left(h_u,h_v,h_w
\right )\)
- 同样的 我们曾经定义过一条射线
- \(Ray \left( P\right ) = O + t \cdot
\vec{u}\)
Ray(P) 射线上某一点O 射线的起点t 沿着方向\(\vec{u}\)前进的长度- \(\vec{u}\) 射线的方向向量
slab method
- 在OBB与光线的求交计算中，我们常用的方法是
slab method
- 将我们测量的这个盒子分成三组平行的板
- 分别将光线与对应的板做相交计算，在射线的方向上，有一个进入这一组板的时间\(t^{min}\)，以及一个出板的时间\(t^{max}\)
- 分别计算对于三个面板的\(t^{min}_{i},t^{max}_{i},i \in
\left(u,v,w\right)\)
- 如果射线与盒子相交，那么简单的说这条射线一定有一段时间是处于这三个\(t^{min},t^{max}\)之中的。
计算原理
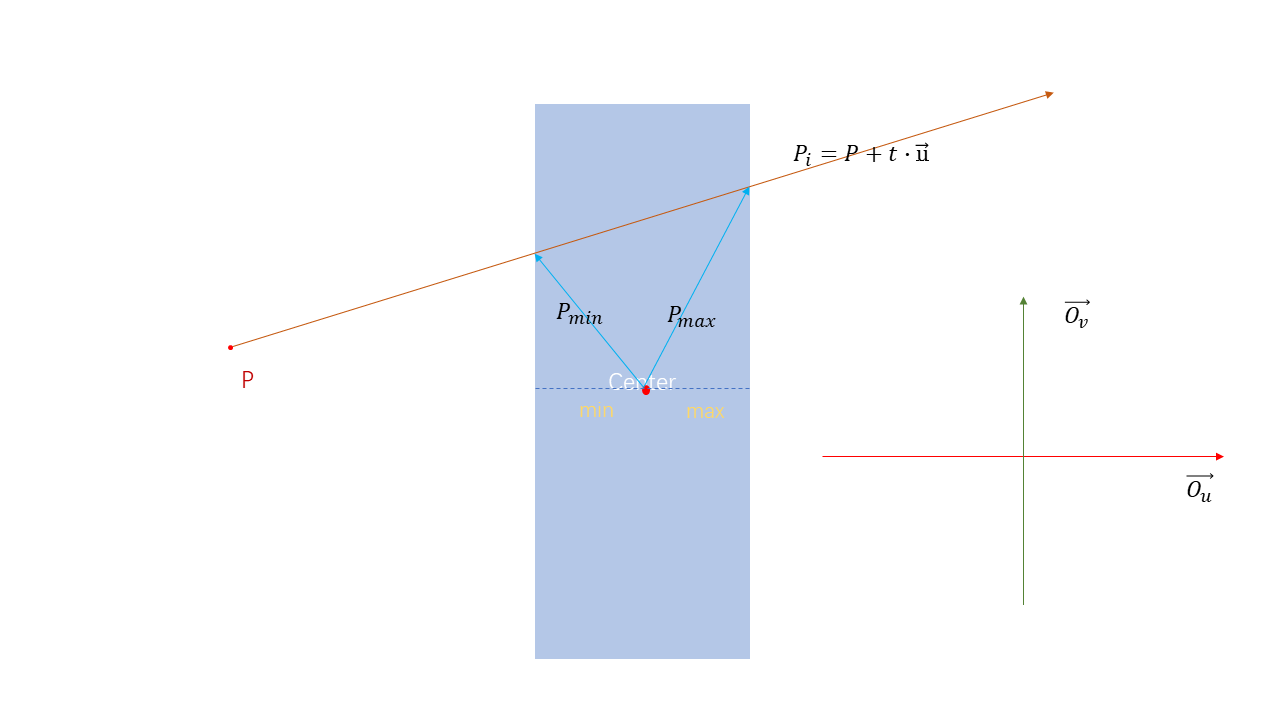intersection
\(P_{min} = P + t_{min} \cdot
\vec{u}\) - \(1.0\)
\(P_{max} = P + t_{max} \cdot
\vec{u}\) - \(1.1\)
\(P_{i} = P + t \cdot \vec{u}\)
- \(1.2\)
$(P_{min} - C ) = min $ - \(1.3\)
$(P_{max} - C ) = max $ - \(1.4\)
\(1.0\)式 & \(1.1\)式 带入 \(1.3\)式 & \(1.4\)式得到： \[
\left [ \left (P + t_i \cdot \vec{u} \right ) - C \right ] \cdot
\vec{O_n} = O_{Size.j} / 2.0, i \in (min,max),j \in (x,y,z), n \in
(u,v,w)
\] => 化简得: \[
t_i = (O_{Size.i} / 2.0 - (C - P) \cdot \vec{O_n}) / (\vec{u} \cdot
\vec{O_n}), i \in (min,max),j \in (x,y,z), n \in (u,v,w)
\]
求交实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
| bool Intersect::IntersectObbWithRay(const OBB& obb, Ray & ray)
{
auto delta = obb.m_center - ray.m_begin;
float t1, t2;
double minT = DBL_MIN, maxT = DBL_MAX;
{
float e = glm::dot(delta, obb.m_u);
float f = glm::dot(ray.m_dir, obb.m_u);
if (std::abs(f) > 1e-20)
{
t1 = (e + obb.m_size.x / 2.0) / f;
t2 = (e - obb.m_size.x / 2.0) / f;
if (t1 > t2)
{
auto temp = t1;
t1 = t2;
t2 = temp;
}
if (t1 > minT)
{
minT = t1;
}
if (t2 < maxT)
{
maxT = t2;
}
if (minT > maxT)
{
return false;
}
if (maxT < 0)
{
return false;
}
}
else if (-e - obb.m_size.x / 2.0 > 0 || -e + obb.m_size.x / 2.0 < 0)
{
return false;
}
}
{
float e = glm::dot(delta, obb.m_v);
float f = glm::dot(ray.m_dir, obb.m_v);
if (std::abs(f) > 1e-20)
{
t1 = (e + obb.m_size.y / 2.0) / f;
t2 = (e - obb.m_size.y / 2.0) / f;
if (t1 > t2)
{
auto temp = t1;
t1 = t2;
t2 = temp;
}
if (t1 > minT)
{
minT = t1;
}
if (t2 < maxT)
{
maxT = t2;
}
if (minT > maxT)
{
return false;
}
if (maxT < 0)
{
return false;
}
}
else if (-e - obb.m_size.y / 2.0 > 0 || -e + obb.m_size.y / 2.0 < 0)
{
return false;
}
}
{
float e = glm::dot(delta, obb.m_w);
float f = glm::dot(ray.m_dir, obb.m_w);
if (std::abs(f) > 1e-20)
{
t1 = (e + obb.m_size.z / 2.0) / f;
t2 = (e - obb.m_size.z / 2.0) / f;
if (t1 > t2)
{
auto temp = t1;
t1 = t2;
t2 = temp;
}
if (t1 > minT)
{
minT = t1;
}
if (t2 < maxT)
{
maxT = t2;
}
if (minT > maxT)
{
return false;
}
if (maxT < 0)
{
return false;
}
}
else if (-e - obb.m_size.z / 2.0 > 0 || -e + obb.m_size.z / 2.0 < 0)
{
return false;
}
}
return true;
}
|