射线与平面相交

计算射线与平面的相交

• 定义平面
• 定义射线
• 解方程

1. 平面方程

1.1 平面方程

• \(p\)为平面上一点，且 \(p = (x,y,z)\)

• 标量表示： $ ax + by + cz = d $

• 矢量表示： $ p = d$

  • \(\vec{n} = [a,b,c]\)
  • 已知任意平面上一点\(p\)即可以求得 $ d $

• 法线 \(\vec{n}\) 决定平面的方向

• \(d\) 定义平面的位置,从原点到平面的有符号的距离

  • 此距离表示沿着法线方向滑动，法线方向上的测量
  • \(d > 0\),原点位于平面背面，反之位于正面

1.2 三个点确定一个平面

• 按照不同的坐标表示给出不同顺序的点
  • 左手系
    • 观察平面的正面，以顺时针给出点的顺序
  • 右手系
    • 观察面的正面，以逆时针给出点的顺序
• 点不能共线
• 三个点在这个确定的平面上

2. 射线与平面求交

• 前处理

  • 射线与平面是否平行(重合)

• 射线方程

• 平面的表示

• 解方程

2.1 射线定义

• 定义射线的起点 \(P_0 = (x,y,z)\)

• 射线的方向\(\vec{u}\)

• 定义如下: \(P = P_0 + t * \vec{u}\)

  • \(P\)为射线上任意一点

  • \(t\)为从起点\(P_0\)沿着方向\(\vec{u}\)前进的距离

2.2 平面定义

• 已知平面法线与平面上任意向量的点击结果为 0

• 取平面上任意点\(P_1,P_2\)，平面法线 \(\vec{n}\)

• 可得：$ = 0 $

2.3 射线与平面的平行计算

射线与平面求交

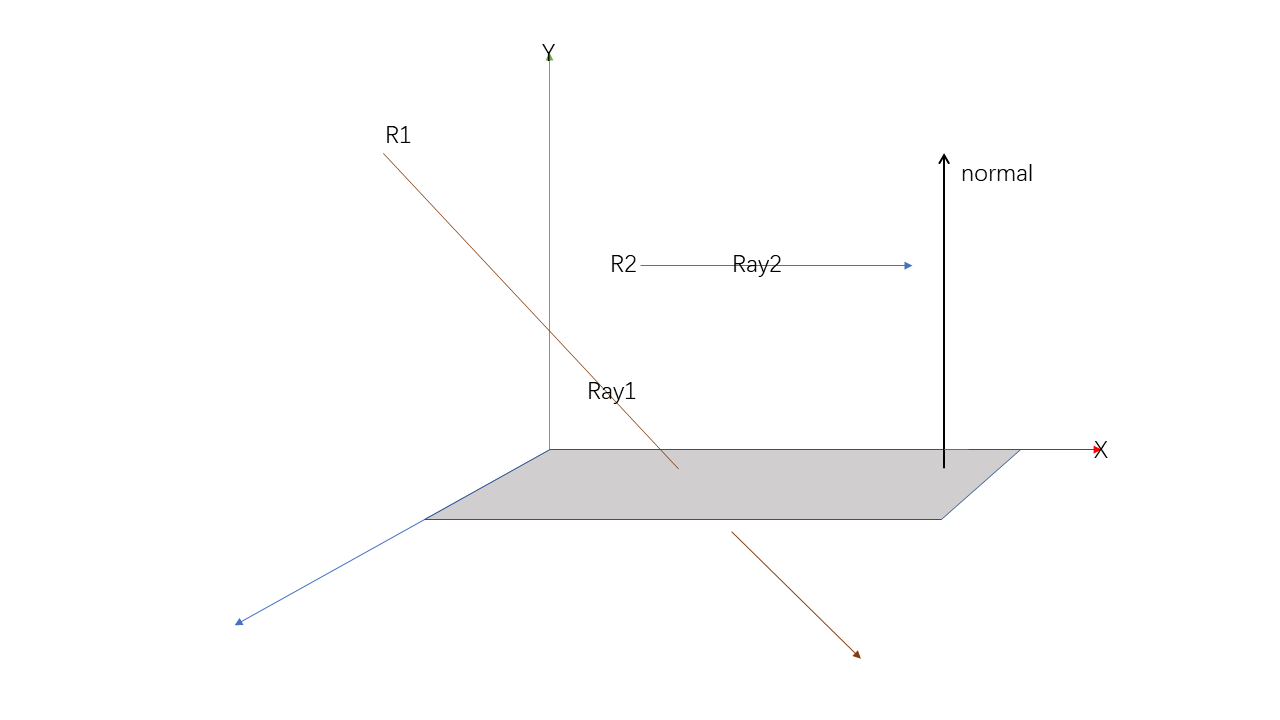
• 判断射线\(Ray_2\)与平面的关系
  • 起点 \(R_2\)

平行判定

• \(Ray_2 \cdot \vec{n} = 0\)
  • 可知射线\(Ray_2\)与平面平行

重合判定

• 已知平面一点 \(P\)

• 射线起点\(R_2\)

• 得：

  • \((P - R_2) \cdot \vec{n} < 0\)
  • 可知\(R_2\)与点\(P\)不共面
  • 可知射线\(Ray_2\)与平面平行

2.4 相交计算

• 除去平行与重合的情况，便只剩下相交与不相交

• 射线 \(P = P_0 + t * \vec{u}\)

• 平面 $ = 0 $

• 若射线与平面相交，则我们取：

  • $ P_1 = P_0 + t * $

=> 带入到平面方程得: \[(P_2 - (P_0 + t*\vec{u})) \cdot \vec{n} = 0\]

\[(P_2 - P_0) \cdot \vec{n} - t * \vec{u} \cdot \vec{n} = 0\]

\[ t = \frac{ (P_2 - P_0)\cdot\vec{n}} {\vec{u}\cdot\vec{n}}\quad \]

• 若 t > 0则射线与平面相交，反之不相交