Normal Matrix

法线矩阵

• 在渲染管线的处理过程中，顶点处理阶段会通过模型变换将局部坐标变换到世界坐标,在模型变换的过程中，顶点会经过旋转、缩放、平移的过程.

• 法线是和方向相关的向量，所以平移对法向这个方向向量是没有意义的，所以我们考虑的是顶点的旋转与缩放对法线的影响，由于法线属于协变矢量(我们将在后面介绍这个概念)的一种，它不能和顶点使用相同的变换矩阵进行变换.

• 为了正确的变换法线，我们必须使用一个和顶点变换矩阵不同的矩阵.

  • 如果矩阵不包含缩放,无疑，它是合适的，可以安全的变换矩阵

    

    不包含缩放的变换

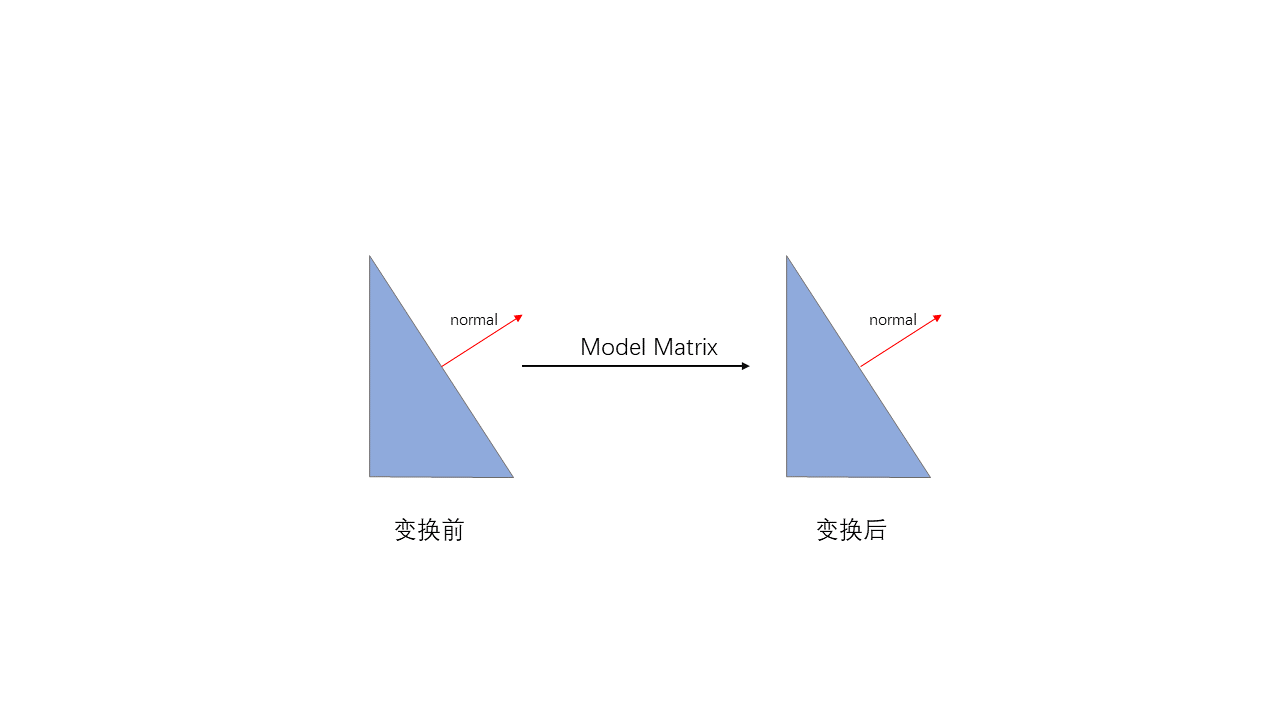
  • 如果矩阵包含均匀的缩放，它仍旧是安全的，依旧可以用来变换法线，唯一需要做的就是，就是变换完成后重新对法线进行归一化.

    

    均匀缩放

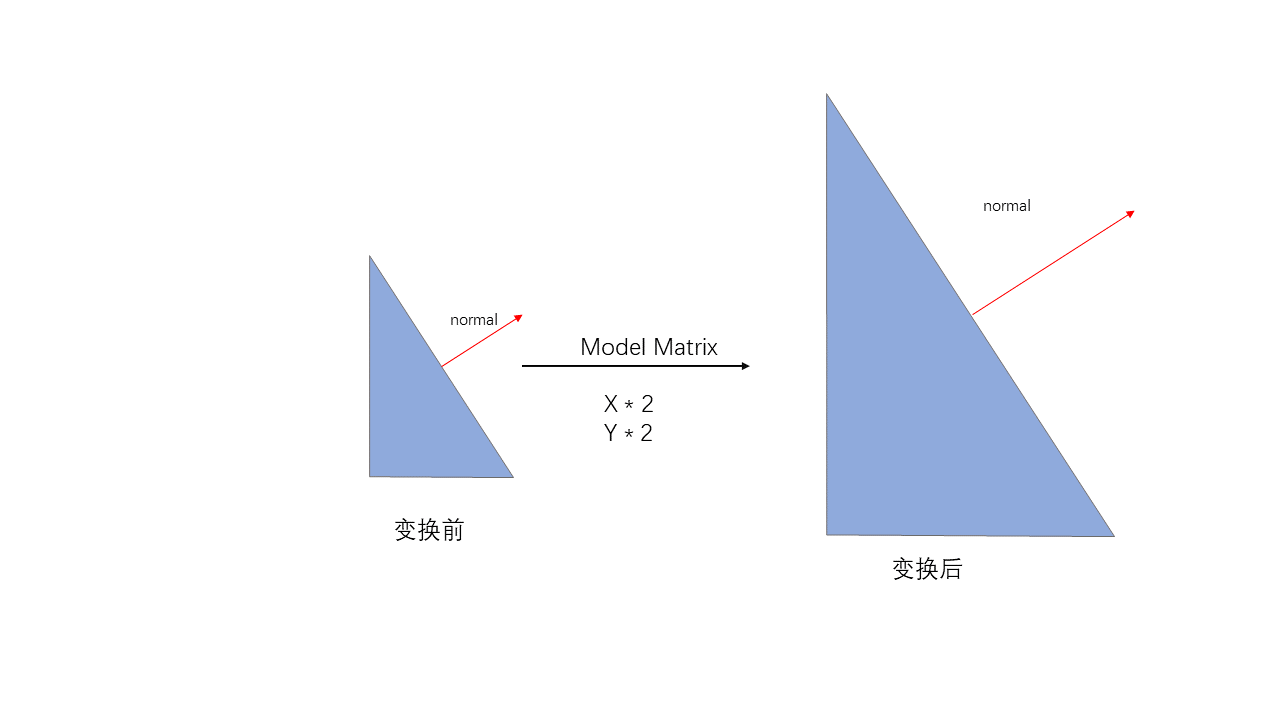
  • 如果矩阵包含非均匀的缩放,我们需要一个新的矩阵处理变换后顶点的法相.

    

    非均匀缩放

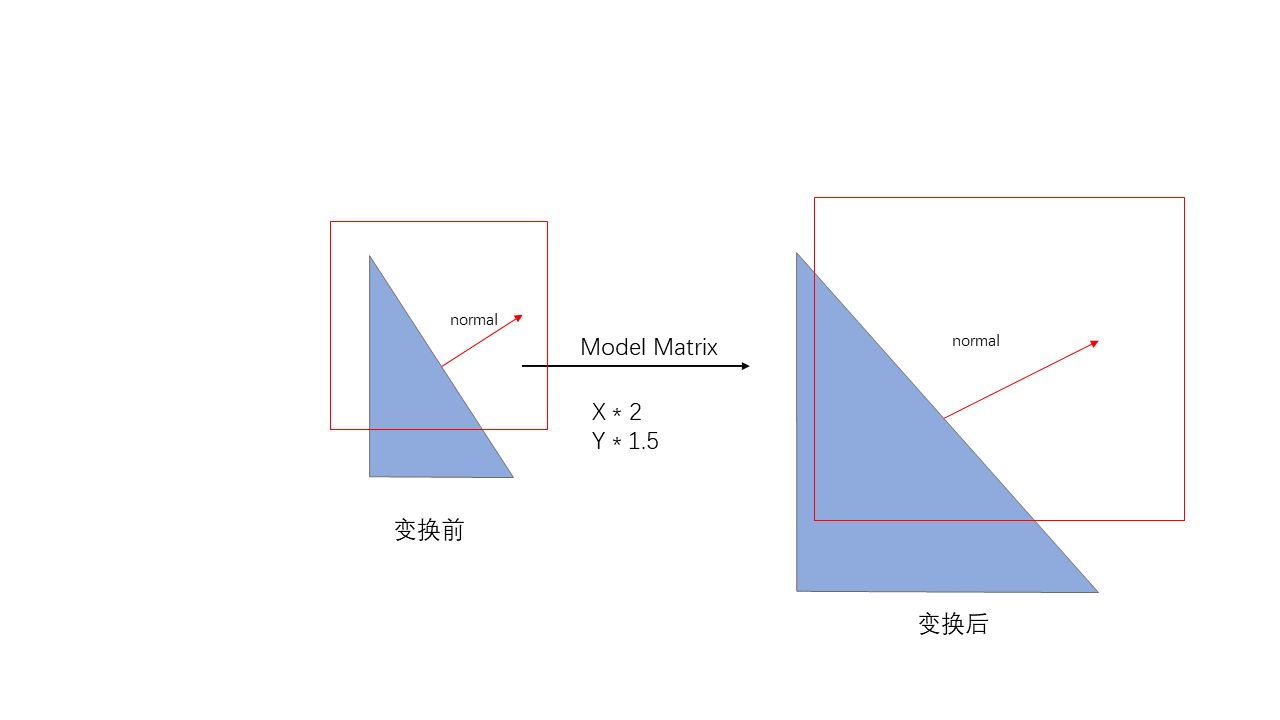
1. 非均匀缩放的法线变换

• 通常情况下，我们在世界空间计算光照等

Normal Matrix

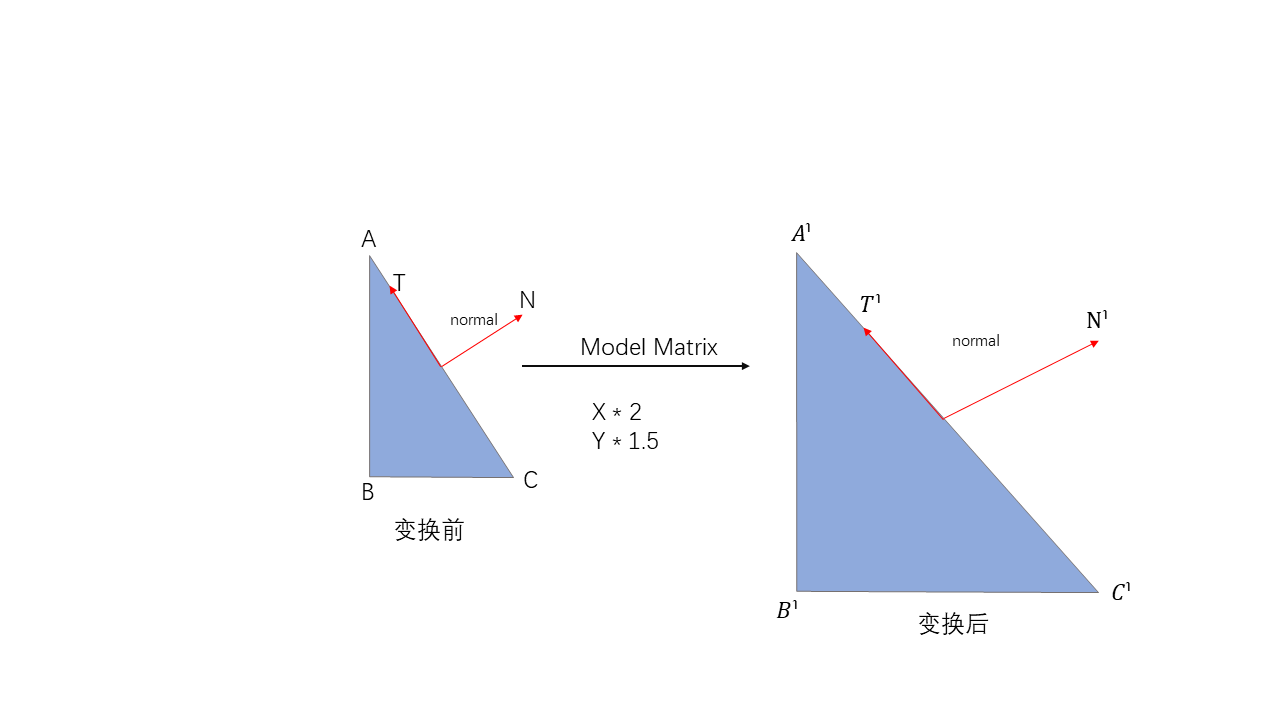
• 推导：

• $\overrightarrow{T}$表示的是${\mathrm{\Delta }}_{ABC}$的切向量，由$A-C$计算得到.

  • $\overrightarrow{N}\mathrm{\perp }\overrightarrow{T}$

• $\overrightarrow{T^{\prime }}$表示的是${\mathrm{\Delta }}_{A^{\prime }{B}^{\prime }{C}^{\prime }}$的切向量，由$A^{\prime }-C^{\prime }$计算得到.

  • 使用相同的变换矩阵之后，$\overrightarrow{N^{\prime }}\cancel{\mathrm{\perp }}\overrightarrow{T^{\prime }}$

• 我们使用 $M$表示模型矩阵

  • $T=vec4(x,y,z,w)$

  $T\times M=(A-C)\times M$

  $T\times M=A\times M-C\times M$

  $T^{\prime }=A^{\prime }-C^{\prime }$

  • $A^{\prime }and{C}^{\prime }$是三角形变换后的顶点，所以$T^{\prime }$仍旧是三角形变换后的切线

• $M$不能用来变换法线，我们只能通过法线$\overrightarrow{N}\cdot \overrightarrow{T}=0$的性质来完成下面的推导

  • 可得$\overrightarrow{N^{\prime }}\cdot \overrightarrow{T^{\prime }}$
  • 法线与切线垂直

• 法线是方向向量，平移对此没有意义，所以我们只考虑模型矩阵的左上角$3\times 3$部分矩阵$M^{\prime }$,并且变换后的法线 $\overrightarrow{N^{\prime }}$ 满足$\overrightarrow{N^{\prime }}\cdot \overrightarrow{T^{\prime }}=0$

• 在我们不知道一个合适的法线变换的矩阵的时候不妨设它$G$

• 此处我们不考虑平移

推导：

​ $\overrightarrow{N^{\prime }}\cdot \overrightarrow{T^{\prime }}=(G_{3\times 3}\times \overrightarrow{N})\cdot (M_{3\times 3}\times \overrightarrow{T})=0$

$(G_3)(M_3)=(G_3{)}^T(M_3)$

${\overrightarrow{N}}^T{G}_{3\times 3}^T{M}_{3\times 3}\overrightarrow{T}=0$

${\overrightarrow{N}}^T\times \overrightarrow{T}=\overrightarrow{N}\cdot \overrightarrow{T}=0$

$G_{3\times 3}^T{M}_{3\times 3}==I$ -- 单位矩阵

$G_{3\times 3}^T==I\ast M_{3\times 3}^{-1}$

$G_{3\times 3}==I\ast (M_{3\times 3}^{-1}{)}^T=(M_{3\times 3}^{-1}{)}^T$